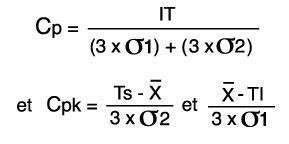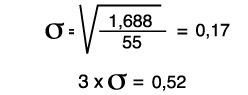Maîtrise des processus : capabilité des lois normales

Capabilité: Application des méthodes statistiques à la qualité en production

Capabilité par Gaston Mougin © 1998

Généralités sur la capabilté et son utilité

La multiplication des échanges économiques de produits de prestations ou de services rend de plus en plus indispensable la mesure de la qualité.
Faire des constats objectifs, concevoir et maîtriser les processus, mesurer les progrès ou les échecs, trouver les causes de non qualité, fixer des objectifs mobilisateurs, sont des activités qui nécessitent des chiffres. Il faut alors les analyser de façon à en extraire le plus de renseignements possibles en utilisant les outils
statistiques appropriés, comme par exemple :
Traitement des données ­ échantillonnages ­ maîtrise statistique du procédé ­ plans d’expériences ­ fiabilité (qualité dans le temps)…
Cette rubrique, présentée sous forme de fiches techniques, comportera alternativement 2 parties :

1) Application de la capabilité

Cas concrets rencontrés en entreprise, avec l’explication théorique et un exemple d’application.

– indices d’aptitude des lois de distribution non symétriques,
– Cartes de contrôle dans le cas de petites séries,
– Exemple d’application d’un plan d’expériences en injection plastique,
– Cartes de contrôle et leurs applications Shewhart, Cusum, Ewma,
– Comparaison des référentiels FORD et CNOMO.

2) Découverte de la capabilité

Révision des principes statistiques de base :

– fonctions de distribution,
– lois statistiques diverses,
– fonction perte de Taguchi,
– corrélation et régression,
– …

Applications statistiques Fiche n°1

Indice d’aptitude dans le cas des lois de distribution non symétriques.
Certains procédés génèrent des dispersions asymétriques et le calcul de l’écart type n’est plus applicable, il est donc impossible de déterminer la capabilité réelle du processus ou du moyen (Cm, Cmk, Cp, Cpk).
Pour détourner cette difficulté, deux méthodes simples sont applicables :
– Méthode graphique par la droite de Henry.
– Méthode du mode.

Méthode graphique

Comme pour les lois de distribution gaussiennes, on utilise la méthode du tracé de l’histogramme sur des échelles Gausso-arithmétiques adaptées à une loi asymétrique (droite de Henry).

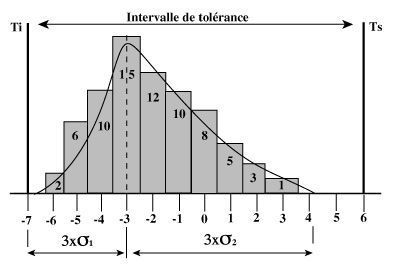
Méthode du mode

Cette méthode consiste à déterminer la loi normale sous-jacente par le mode.

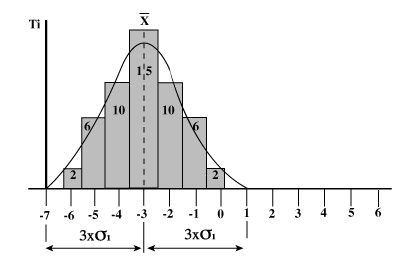
Soit l’histogramme asymétrique ci-dessus, pour calculer la loi normale sous-jacente représentative de la partie gauche de la dispersion, il suffit de calculer s1 en coupant l’histogramme par le mode et en le dupliquant.

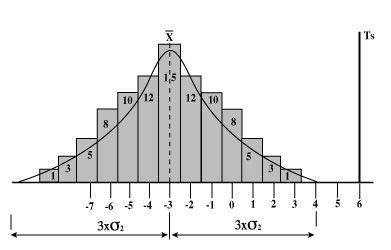
idem pour s2

Les indices d’aptitudes seront :

Exemple d’application :
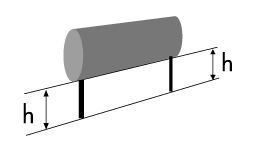
Mesure de la hauteur des pattes d’un produit électronique destiné à être inséré dans un circuit imprimé.

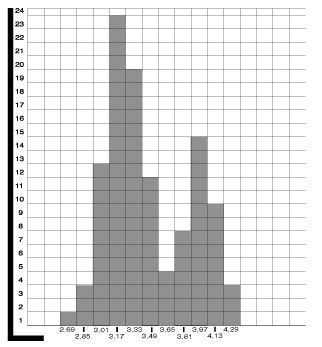
Classement des résultats des mesures

La distribution montre une bimodalité due à une différence de longueur moyenne entre les 2 pattes (une des pattes a une longueur moyenne de 3,17 ; l’autre de 3,97).

Calcul de la dispersion selon la méthode du mode, côté mini :

(2,69 ­ 3,17)2 x 1 = 0,230
(2,85 ­ 3,17)2 x 3 = 0,307
(3,01 ­ 3,17)2 x 12 = 0,307
(3,17 ­ 3,17)2 x 23 = 0,000
(3,33 ­ 3,17)2 x 12 = 0,307
(3,49 ­ 3,17)2 x 3 = 0,307
(3,65 ­ 3,17)2 x 1 = 0,230

Valeur mini 3,17 ­ 0,52 = 2,65 mini

Le calcul côté maxi nous donne :

3,97 + 0,51 = 4,48 maxi

la dispersion totale est 4,48 ­ 2,65 = 1,83 mm, le calcul des capabilités est alors possible.

Conclusion sur la capabilité des lois normales

La dispersion individuelle de chacune des longueurs est correcte ; il suffit de régler la machine pour confondre les longueurs individuelles.

Bibliographie autour de la capabilité

Maîtrise statistique des processus – Maurice Pillet ­ éditions d’Organisation