La fonction perte de Taguchi
Dans de nombreux cas l’intervalle de tolérance représente le contact qui permet de déterminer si un produit est conforme ou non.
Toutefois si l’on raisonne en terme de performance ou de coût il est nécessaire de considérer la situation de chaque produit par rapport à l’objectif (l’objectif est considéré ici comme le produit le plus performant au meilleur coût)
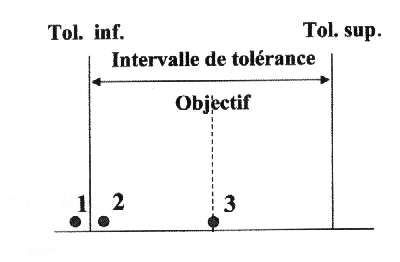
Si l’on considère la position des pièces 1, 2 et 3 par rapport aux limites de tolérances (figure 1) la question suivante se pose :
En terme de conformité, quelle est la différence entre la pièce 1 et la pièce 2. ?
Réponse, il n’y en a pas, toutes les deux sont conformes.
Quelle est la différence entre la pièce 2 et 3 ?
Réponse : Elle est importante car la pièce 2 est conforme alors que la pièce 3 n’est pas conforme.
Pourtant si l’on considère la différence entre les caractéristiques, il y a plus de différence entre 1 et 2 qu’entre 2 et 3.
De plus la position de la tolérance inférieure pourrait sans risques être déplacée légèrement à gauche ou à droite sans affecter la qualité globale.
Ce qui rendront 2 et 3 tous les deux conformes ou tous les deux non-conformes.
Ces limites, ne paraissent en effet pas très adaptées et Taguchi a proposé la solution suivante :
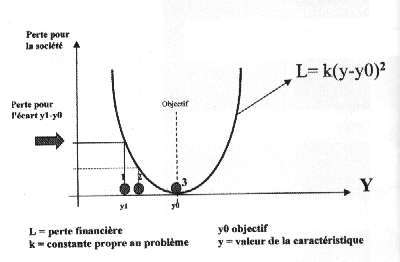
» tout écart par rapport à l’objectif engendre une perte financière (pour le client ou en interne) égale au carré de l’écart à l’objectif « , ce qui se traduit par le schéma suivant
La détermination économique des tolérances
Exemple : dans la fabrication d’un escalier en bois une des opérations consiste à maîtriser la largeur de la rainure dans laquelle vient s’encastrer et se coller la marche.
Jeu souhaité : 0,2 mm (objectif)
Jeu trop grand : la colle ne remplit pas son office
Jeu trop petit : la colle est refoulée
L’entreprise a évalué que pour un jeu de 0,45 mm le remplacement est systématique et coûte 400 francs chez le client.
Le coefficient k de la perte de Taguchi vaut alors :
400 frs = k (0.45-0.2)² soit 6400
On peut alors calculer la tolérance économique pour le traitement d’un défectueux estimé à 150 francs en fabrication
150 frs = 6400 (Y-0.2) soit 0.35 mm pour Y.
Le gain financier de l’amélioration de la capabilité
En reprenant notre exemple, la dispersion due à la machine suit la loi normale de 0.1 mm d’écart type. Après une action d’amélioration celui-ci passe à 0.03 et est centré sur l’objectif de 0.2 mm.
Le gain est alors de L = k ( 1² – 2²)
L = 6400 (0.1² – 0.03²) = 58.24 francs par marche d’escalier produite.
Conclusions
Cette approche économique des limites de tolérances et de la dispersion est un changement de culture. En effet, il ne suffit pas que les pièces soient à l’intérieur des limites de tolérances, il faut également une répartition centrée sur l’objectif et une dispersion la plus faible possible.